alistat

1.1.2 Concept and Actors

Competitions have two actors roles:

Petitioner

The individual who poses a problem and initiates a competition

Creator

The individual who proposes a solution accompanied by a proof

There is no role of “reviewer” as solutions are validated by the platform.

We focus on algorithmic problems, thus petitioners provide definitions of algorithmicproblems while creators provide algorithms. A definition for an algorithmic problem consist of the following:

• A definition for the underlying computational problem which will serve as a specification for the correctness of proposed algorithms
• A set of complexity constraints that must be satisfied by proposed algorithms

Creators submit algorithms in the form of a procedural program and accompany them with a proof for their correctness and their worst case asymptotic complexity. Proofs are composed with the utilization of formal program verification methods.

3.1.2 Competition flow

The main flow of a completion is as follows:

1. The petitioner submits the question q, initiating the competition
2. A creator submits an answer a accompanied by a proof p
3. The system invokes the proof validator* v on (q, a, p) and
   1. if v responds positively the competition concludes successfully
   2. otherwise, the system allows the re-execution of step 2

This flow is depicted in figure 3.1.

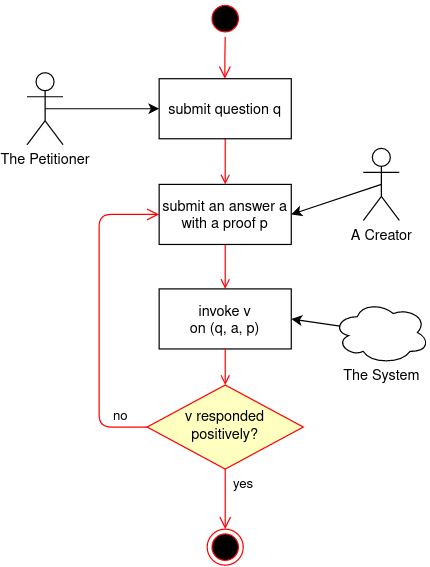
* See Definition 3.2 of the full text for proof validators

3.2.2 Solver algorithms/Answer objects (simplified)

Solver algorithms/Answer objects are represented as procedural programs having the solve function.

Here is an example of a solver for the natural square root of natural numbers. The result will be -1 if there is no natural square root.

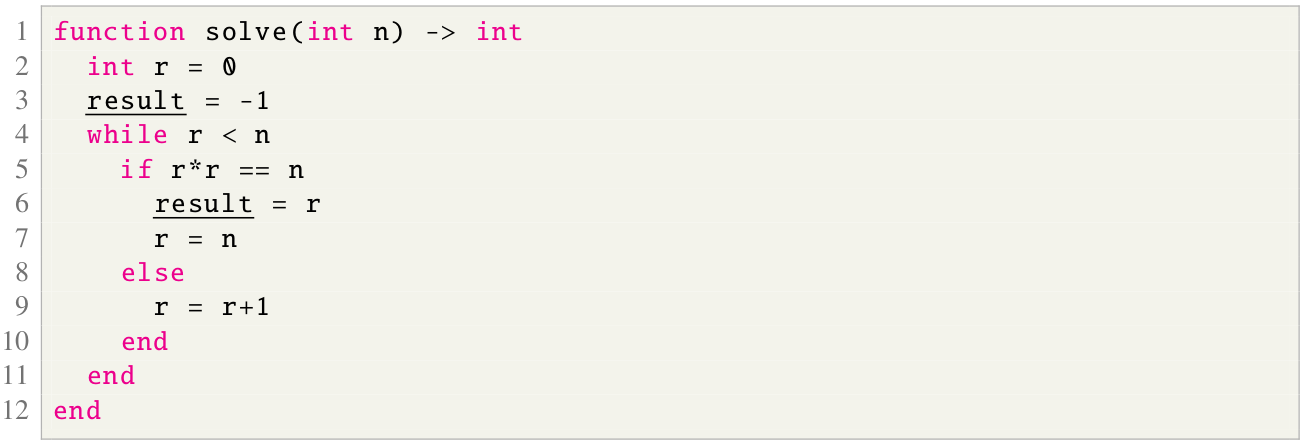
3.2.3 Problem definitions/Question objects (simplified)

To define an algorithmic problem* we create a program necessarily containing the following funcions:

validInstance(i)

Determines whether instance i is a valid instance of the problem

negatedVerify(i, s, h)

Determines whether solution s is not correct for instance iwith the help of hint h

The negatedVerify function must behave as follows:

• If s is correct for i then it must return false for every h
• If s is not correct for i then there must exist an h for which it returns true

Example: Here is a definition for the natural square root problem.

This example behaves as follows:

• If s is -1, meaning there is no square root, the hint should provide the actual square root to prove the mistake
• Otherwise, it compares s with the square of i to check if s is not the actual square root of i

Negating the verifier seems counter-intuitive, however, it serves for creating proofs of correctness as described in the next section.

* This page focuses on correctness, refer to the full text for details about asymptotic complexity constraints.

3.2.4.2 Correctness (simplified)

To examine the correctness of a given solver against a certain problem definition, we compose the program correctness.

It is proved (Proposition 3.2 and section 3.2.4.2 in the full text) that a candidate solver is correct if and only if

• program correctness terminates for every i and h
• and variable verdict is always true at program termination.

4 System Design and Implementation (overview)

A petitioner must provide two inputs to create a competition:

1. The problem definition
2. The reward amount in eth currency

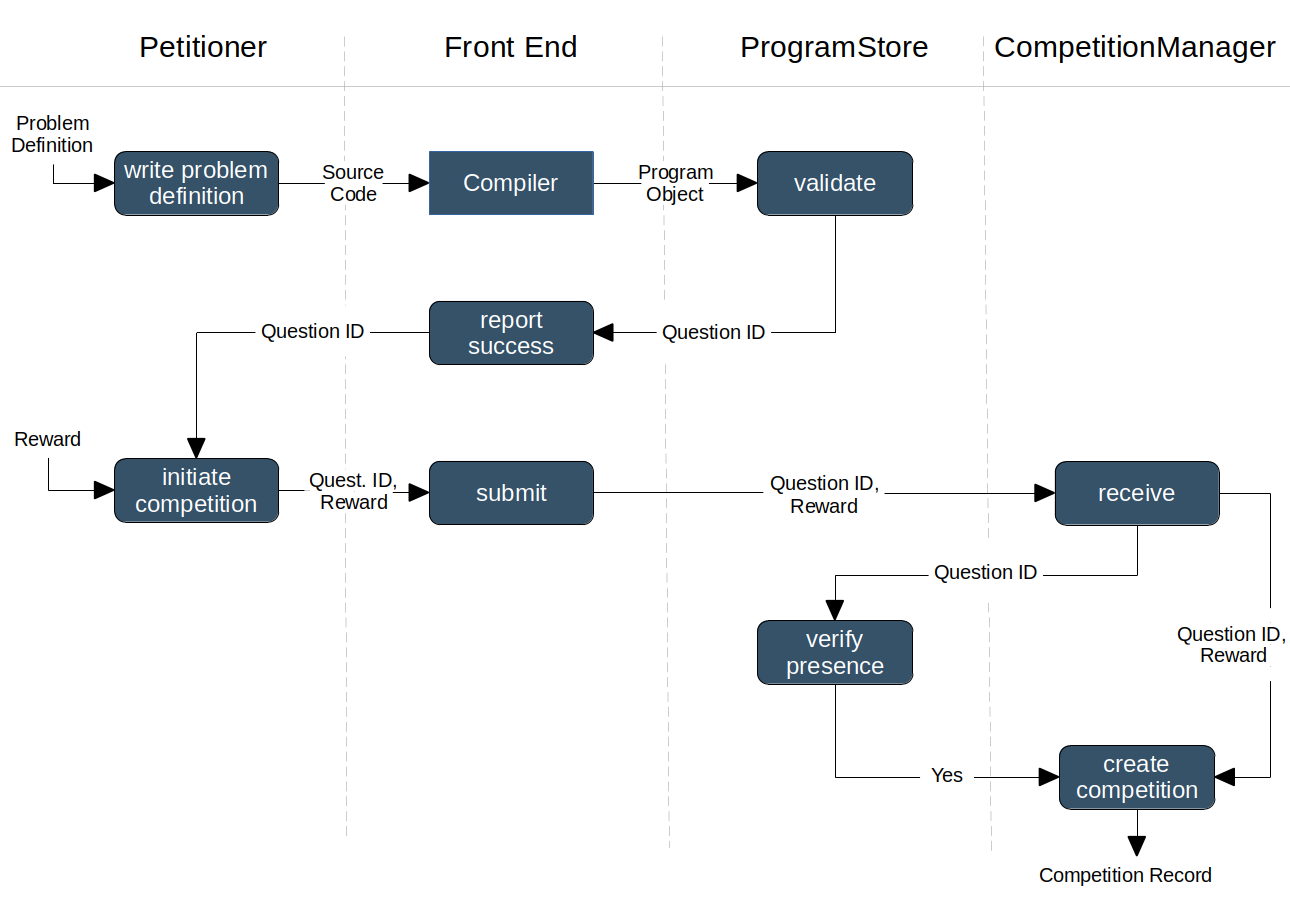
A creator needs to perform two steps to submit a solution:

1. Write the solver algorithm
2. Make the formal proof for the correctness of the solver algorithm against the problem definition

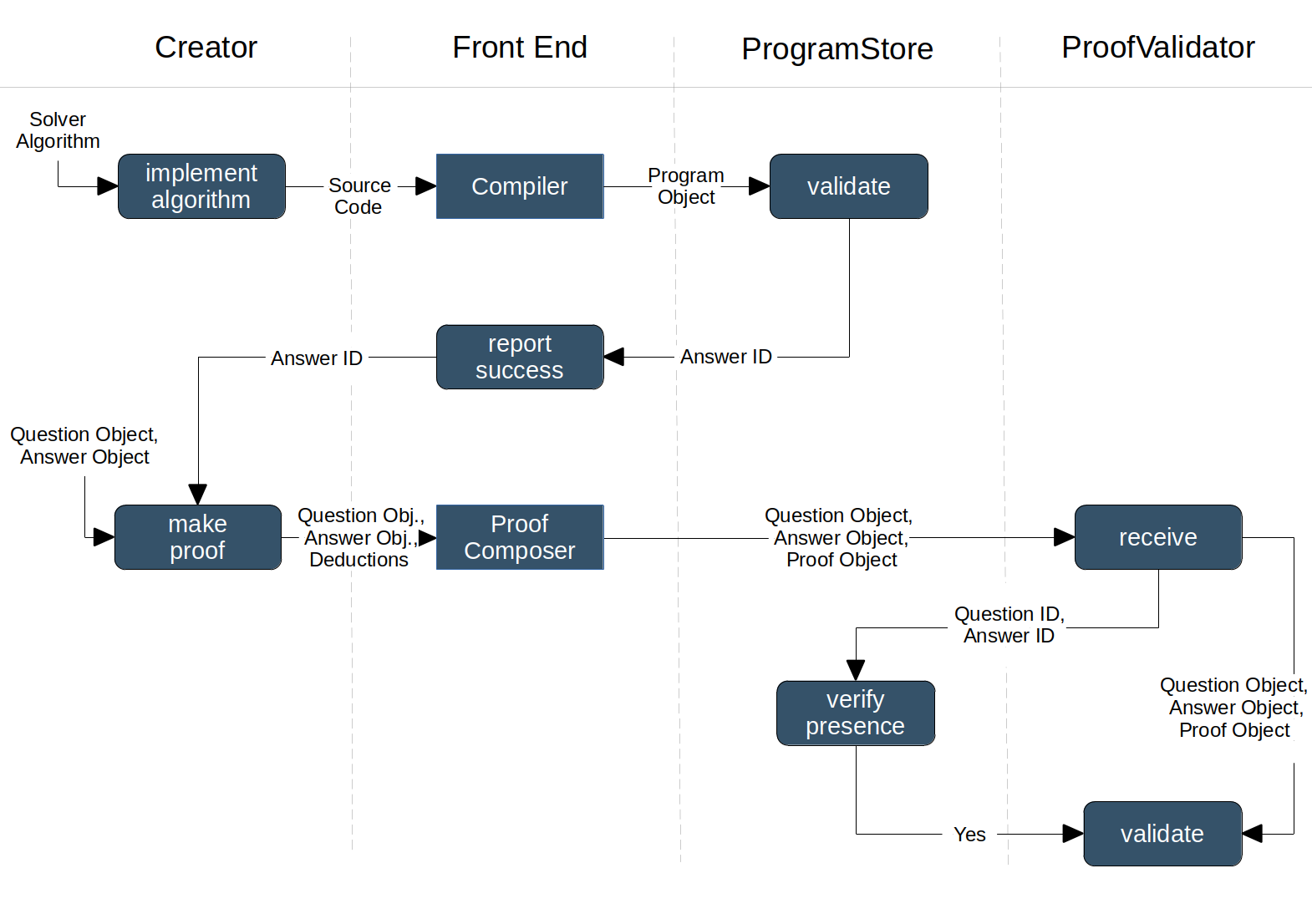
5 Evaluation (a few words)

The proof of concept system is evaluated in terms of the observed length of the proofs and the gas cost (Ethereum computational fees) required to validate them.

6.1 Conclusions

We have proposed a blockchain-based platform design for conducting algorithmic problem solving competitions where proposed algorithms can be mechanically validated. The feasibility of this design has been demonstrated by a proof-of-concept implementation. As part of the design, we proposed a method for representing algorithmic problem definitions as procedural computer programs and showed that these representations can be effectively used to validate the correctness and complexity bounds of proposed algorithms.

The evaluation process revealed two main issues regarding the use of the platform, though none of them is irrecoverable. The first issue arises from the length of the proofs of correctness. The relatively large number of low level deduction steps makes it cumbersome for human users to compose proofs. The second issue arises from the relatively large number of axioms needed for a proof that only relies on simple arithmetic truths. This signals that more complex proofs would require a very large number of axioms or otherwise, they would have to prove many trivial facts thus making the proofs immensely lengthy.